跳跃链表

前言

最近有被问到redis中zset类型的数据结构–跳表，所以本章就跳表的原理及redis中的实现做一个总结。

跳表原理

跳表的结构很简单，就是在一个链表的基础上，建立n层索引层。

如上图所示，借助索引层，可以使得查询按照类似二分查找的方式更快定位目标节点的位置，而不必遍历整个链表。
也因此，跳表中是不允许重复的值的。

实现方式

跳表可以理解为几层链表，只不过一层比一层”稀疏”。实现跳表一个关键点在于确定节点的层数。

// 采用随机的方式确定每一个节点的层数
public int randomLevel() {
    int level = 1;
    int p = 5;
    while (r.nextInt(10) < p && level < MAX_LEVEL) {
        level++;
    }
    return level;
}

类定义

// 跳表节点类
public class SkipListNode {
    // 下一个节点
    private SkipListNode next;
    // 下一层节点
    private SkipListNode down;
    // 节点所在层数
    private int level;
    // 值
    private Integer value;

    public SkipListNode(int level, Integer value) {
        this.level = level;
        this.value = value;
    }

    public SkipListNode(Integer value) {
        this.value = value;
    }
}

这里实现跳表是定义了每一个节点(相同值不同层当作不同节点)，通过节点的next指针和down指针操作。

// 跳表定义
public class SkipList {
    // 最大层数，对层数随机的限制
    private static final int MAX_LEVEL = 16;
    // 头节点，是一个虚节点，无实际值
    private SkipListNode head;
    // 跳表长度，实际值的数量，不包括索引节点
    private int size;
    // 当前跳表最大的层数
    private int maxLevel;
    // 用来随机层数
    private Random r = new Random();

    // 构造方法，初始化头节点
    public SkipList() {
        this.head = new SkipListNode(1, 0);
        this.head.setNext(null);
        this.head.setDown(null);
        this.size = 0;
        this.maxLevel = 1;
    }

基本操作

// 新增操作
public void insert(Integer value) {
    // 校验，不让插重复值
    if (find(value)) {
        System.out.println("值已存在");
        return;
    }
    // 1. 随机计算新节点层次
    int currentMaxLevel = randomLevel();
    // 2. 遍历每一层插入节点
    // 2.1 判断当前最大层次是否满足
    if (currentMaxLevel > maxLevel) {
        for (; maxLevel < currentMaxLevel; maxLevel++) {
            SkipListNode newHead = new SkipListNode(maxLevel + 1, null);
            newHead.setDown(head);
            head = newHead;
        }
    }
    // 2.2 取头节点作为游标
    SkipListNode cursorHeadNode = head;
    // 2.3 新建节点
    SkipListNode newNode = new SkipListNode(maxLevel, value);
    // 2.4 循环处理
    for (int i = maxLevel; i > 0; i--) {
        SkipListNode cursorNode = cursorHeadNode.getNext();
        // 当前层次大于新建节点最大层次，下降一层并跳过
        if (i > currentMaxLevel) {
            cursorHeadNode = cursorHeadNode.getDown();
            continue;
        }
        // 当前层次遍历
        while (true) {
            // 头节点的下一节点为空
            if (cursorNode == null) {
                cursorHeadNode.setNext(newNode);
                break;
            }
            // 第一个节点值比新增值大
            if (cursorNode.getValue() > value) {
                cursorHeadNode.setNext(newNode);
                newNode.setNext(cursorNode);
                break;
            }
            if (cursorNode.getValue() < value) {
                if (cursorNode.getNext() == null) {
                    // 跟在最后一个节点后面
                    cursorNode.setNext(newNode);
                    break;
                }
                if (cursorNode.getNext().getValue() > value) {
                    // 插入两者中间
                    newNode.setNext(cursorNode.getNext());
                    cursorNode.setNext(newNode);
                    break;
                }
            }
            // 移动到下一节点
            if (cursorNode.getNext().getValue() < value) {
                cursorNode = cursorNode.getNext();
            }
        }
        cursorHeadNode = cursorHeadNode.getDown();
        // 设置新节点的下一节点
        SkipListNode nextNewNode = new SkipListNode(i - 1, value);
        newNode.setDown(nextNewNode);
        newNode = nextNewNode;
        if (i == 1) {
            size++;
        }
    }
}

// 查询
public boolean find(Integer value) {
    // 游标节点
    SkipListNode cursorNode = head;
    while (true) {
        // 游标为null，终止遍历
        if (cursorNode == null) {
            return false;
        }
        // 头节点为虚节点，所以取下一节点为当前节点与入参做比较
        // 或 已经比较过的节点作为游标，所以也是取他的下一节点做比较
        SkipListNode currentNode = cursorNode.getNext();
        if (currentNode == null) {
            cursorNode = cursorNode.getDown();
            continue;
        }
        // 比较当前节点与入参的值
        if (currentNode.getValue().equals(value)) {
            return true;
        }
        if (currentNode.getValue() > value) {
            // 当前节点大，游标移动到下一层
            cursorNode = cursorNode.getDown();
            continue;
        }
        if (currentNode.getValue() < value) {
            // 当前节点小，下一节点为空，则移动到下一层
            if (currentNode.getNext() == null) {
                cursorNode = currentNode.getDown();
                continue;
            }
            // 当前节点小，下一节点不为空但比入参大，移动到下一层
            if (currentNode.getNext().getValue() > value) {
                cursorNode = currentNode.getDown();
                continue;
            }
            // 当前节点小，下一节点不为空且也比入参小，游标移动到下一节点
            if (currentNode.getNext().getValue() < value) {
                cursorNode = currentNode.getNext();
                continue;
            }
        }
    }
}

以一个个节点实现跳表逻辑的时候发现相比用数组维护同一值的结构，操作要复杂一些。因为会涉及节点的比较及右移，下移。

测试

 public void skipListTest() {
    SkipList list = new SkipList();
    list.insert(1);
    list.insert(5);
    list.insert(9);
    list.insert(12);
    list.insert(3);
    list.insert(34);
    list.insert(20);
    list.insert(11);
    list.insert(6);
    list.insert(8);
    list.insert(2);
    list.insert(4);
    list.insert(33);
    list.insert(21);
    list.insert(19);
    list.insert(25);
    list.insert(72);
    list.insert(13);
    list.insert(15);
    list.insert(7);
    list.insert(32);
    logger.info("size;{}", list.getSize());
    list.showData();
}

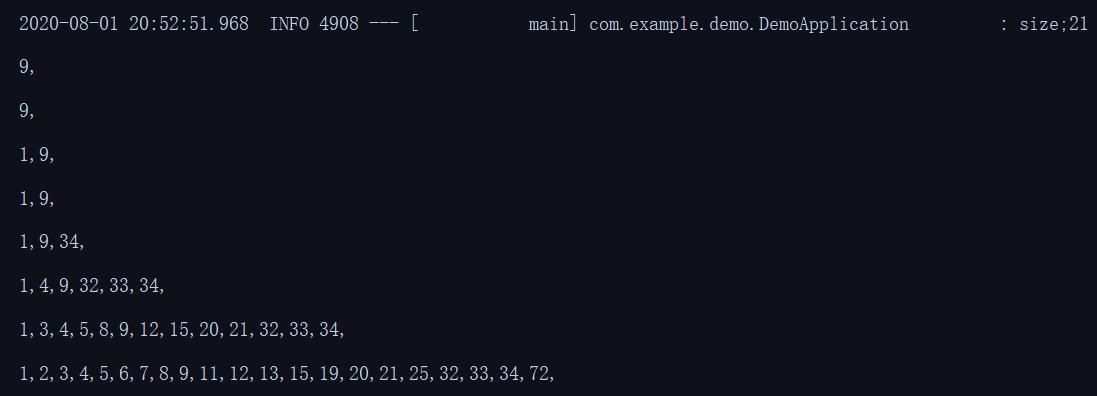
测试发现，因为每个新节点的层数都是按照随机的方式决定，那么有可能会导致索引层的不合理。

redis实现

先来看看redis的节点定义

typedef struct zskiplistNode {
    // 成员对象
    robj *obj;
    // 分值
    double score;
    // 后退指针
    struct zskiplistNode *backward;
    // 层
    struct zskiplistLevel {
        // 前进指针
        struct zskiplistNode *forward;
        // 跨度
        unsigned int span;
    } level[];
} zskiplistNode;

redis的节点定义与上述例子不同，他是在节点内用数组维护了对应层的下一节点。
借用这种思想用Java实现的话：

// 节点类
public class SkipListNode2 {

    private Integer value;

    private Integer level;
    /**
     * 对应每一层的下一节点
     */
    private SkipListNode2[] nextNodes;

    public SkipListNode2(int level) {
        this.value = -1;
        this.level = level;
        this.nextNodes = new SkipListNode2[level];
    }

    public Integer getValue() {
        return value;
    }

    public void setValue(Integer value) {
        this.value = value;
    }

    public Integer getLevel() {
        return level;
    }

    public void setLevel(Integer level) {
        this.level = level;
    }

    public SkipListNode2[] getNextNodes() {
        return nextNodes;
    }

    public void setNextNodes(SkipListNode2[] nextNodes) {
        this.nextNodes = nextNodes;
    }
}

// 跳表类
public class SkipList2 {
    private static final Logger logger = LoggerFactory.getLogger(SkipList2.class);

    private static final int MAX_LEVEL = 16;

    private Random r = new Random();

    private int levelCount;

    /**
     * 头节点
     */
    private SkipListNode2 head;

    public SkipList2() {
        this.levelCount = 1;
        this.head = new SkipListNode2(MAX_LEVEL);
    }

    /**
     * 插入节点
     *
     * @param value
     */
    public void insert(Integer value) {
        if (find(value) != null) {
            logger.info("值已存在");
            return;
        }
        int level = randomLevel();
        SkipListNode2 newNode = new SkipListNode2(level);
        newNode.setLevel(level);
        newNode.setValue(value);
        SkipListNode2[] newNextNodes = new SkipListNode2[level];
        newNode.setNextNodes(newNextNodes);
        // 游标节点
        SkipListNode2 cursorNode = head;
        for (int i = level - 1; i >= 0; i--) {
            // 比较下一节点与入参值，若小于入参值则向后移动
            while (cursorNode.getNextNodes()[i] != null
                    && cursorNode.getNextNodes()[i].getValue() < value) {
                cursorNode = cursorNode.getNextNodes()[i];
            }
            // 遍历到大于入参值的节点，置为新节点当前层的下一节点
            newNextNodes[i] = cursorNode.getNextNodes()[i];
            cursorNode.getNextNodes()[i] = newNode;
        }
        if (level > levelCount) {
            levelCount = level;
        }
    }

    /**
     * 搜索
     *
     * @param value
     * @return
     */
    private SkipListNode2 find(Integer value) {
        // 游标节点
        SkipListNode2 cursorNode = head;
        for (int i = levelCount - 1; i >= 0; i--) {
            // 比较下一节点与入参值，若小于入参值则向后移动
            while (cursorNode.getNextNodes()[i] != null
                    && cursorNode.getNextNodes()[i].getValue() < value) {
                cursorNode = cursorNode.getNextNodes()[i];
            }
        }
        if (cursorNode.getNextNodes()[0] != null
                && cursorNode.getNextNodes()[0].getValue().equals(value)) {
            return cursorNode;
        } else {
            return null;
        }
    }

    public void showData() {
        SkipListNode2 cursorNode = head;
        for (int i = levelCount - 1; i >= 0; i--) {
            // 比较下一节点与入参值，若小于入参值则向后移动
            while (cursorNode.getNextNodes()[i] != null) {
                System.out.print(cursorNode.getNextNodes()[i].getValue() + ",");
                cursorNode = cursorNode.getNextNodes()[i];
            }
            cursorNode = head;
            System.out.println();
        }
    }

    /**
     * 随机计算节点最大层次
     *
     * @return
     */
    public int randomLevel() {
        int level = 1;
        int p = 5;
        while (r.nextInt(10) < p && level < MAX_LEVEL) {
            level++;
        }
        return level;
    }
}

这种思路明显要比单一节点的实现更加方便，数组存放了下一节点指针，而不同的下标又表示了不同层的下一节点指针，替代了next和down指针的作用。

小结

  redis用跳表实现zset类型要比上面实现的例子考虑的更多(像节点维护的跨度信息，及zset权重分数
的维护等)，不过本章只探讨跳表的实现思路，所以就不详细探讨这方面了。
  关于跳表的实现我一开始想的是用一个一个节点去描述跳表结构，看了redis的节点定义及网上的一些
示例，才理解用数组去描述的思路。用数组实现的代码看起来有点绕，但是理解了就会觉得很简单，不用
像节点那样频繁的转移。数组使得遍历操作变得更加直接。